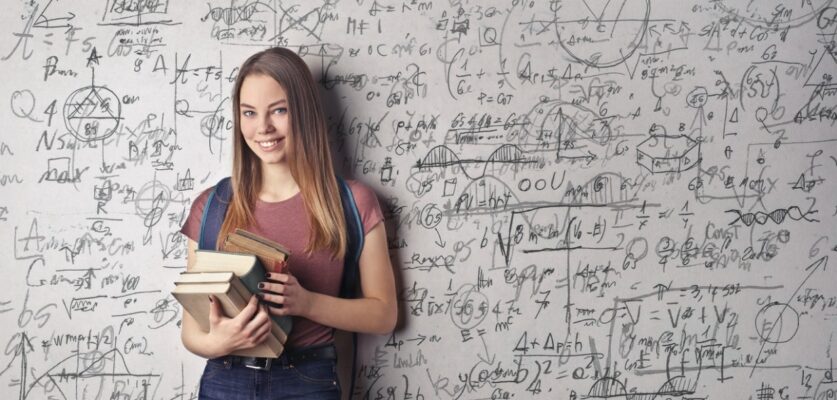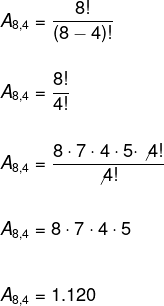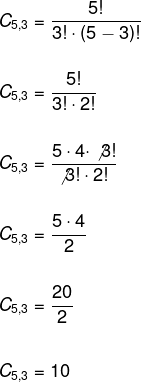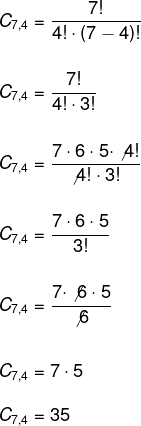Muita gente, quando ouve falar de análise combinatória, lembra imediatamente da época de escola ou faculdade. Porém, precisamos ter cuidado para não cair no erro de achar que ela é “coisa do passado” ou um desses conhecimentos que dificilmente usamos no dia-a-dia. 

Os princípios da análise combinatória são aplicados para obter informações que consumimos diariamente em páginas da Internet, aplicativos que usamos em nossos celulares e até jogos que nos entretêm e desafiam nossas habilidades cognitivas.

A questão é que dificilmente podemos vê-los “em ação”, pois esses processos matemáticos costumam ficar nos “bastidores”. Isto é, não são visíveis para os usuários “comuns”, mas desempenham funções importantes em diferentes campos da ciência e do conhecimento. 

Por exemplo: no estudo das probabilidades e estatísticas, em pesquisas no campo da genética, no registro dos CPFs (que deve ser um número único para cada cidadão), na análise de dados da saúde (por exemplo, na contagem e avaliação dos contágios durante a pandemia de COVID-19), na definição de senhas e sistemas de cibersegurança, etc.  

Por isso, saber como fazer uma análise combinatória e interpretar seus resultados não é importante só para tirar uma boa nota ou passar num concurso, mas também para compreender um amplo leque de informações e porcentagens que nos rodeiam e que, muitas vezes, usamos para tomar decisões no nosso cotidiano. 

Primeiro: o que é a análise combinatória?

A análise combinatória é um ramo dentro das Matemáticas que se dedica à construção e enumeração de propriedades de ordenamento e configurações que satisfaçam certas condições estabelecidas, assim como ao desenvolvimento de métodos de contagem que servem, principalmente, para determinar a quantidade de agrupamentos possíveis para os elementos de um determinado conjunto, seguindo certas regras ou condições específicas. 

Podemos dizer que sua principal razão de ser é permitir o cálculo do número de possibilidades que podem acontecer num determinado evento ou experimento, sem ter a necessidade de descrever cada uma dessas possibilidades. Por isso, torna-se particularmente útil em experiências que envolvem um grande número de possibilidades, onde seria inviável ou demandaria uma enorme quantidade de tempo detalhar, um por um, os resultados possíveis. 

Na imagem abaixo, vemos um exemplo bem simples de possíveis combinações usando apenas as primeiras três letras do nosso alfabeto:

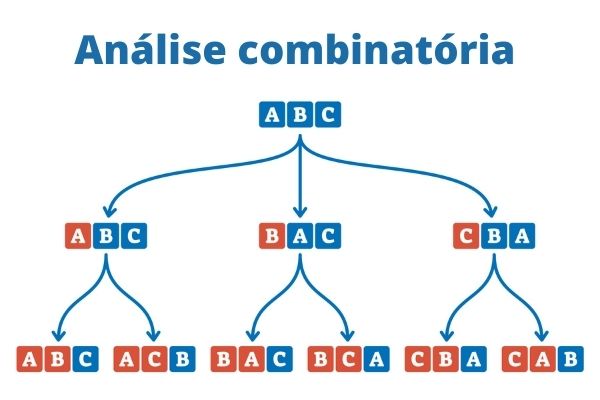
Como podemos perceber, existem várias formas de agrupar elementos, por isso, guiando-se pelo princípio multiplicativo (ou princípio da contagem), foram desenvolvidas diferentes fórmulas de análise combinatória para abarcar cada uma das possibilidades de reagrupamento desses elementos.

Por isso, para fazer uma análise combinatória corretamente, precisamos identificar o tipo de agrupamento proposto, pois, assim, saberemos escolher o método mais apropriado para calcular todas as combinações possíveis. Já já falaremos mais sobre isso, mas, primeiro, precisamos entender bem dois conceitos chave: o princípio da contagem e o fatorial de um número. 

Princípio da contagem e Fatorial: o que significam?

O princípio multiplicativo ou princípio fundamental da contagem (P.F.C.) é um método algébrico para calcular o número total de possibilidades em um determinado experimento ou evento. Nele se baseiam as fórmulas usadas para encontrar os possíveis reagrupamentos ordenados dos elementos de um conjunto. 

Este princípio determina que: 

“Se uma decisão A pode ser tomada de n formas e uma decisão B pode ser tomada de m formas, e essas decisões são independentes, então, o número de combinações possíveis entre essas duas decisões é calculado pela multiplicação n · m.”

Basicamente, isto significa multiplicar o número de possibilidades de cada etapa do experimento para encontrar o número total de possibilidades em todo o processo. Para entender melhor, veja a imagem abaixo:

E o fatorial de um número?

Já o fatorial (representado por n!) nada mais é que uma forma de decompor um número natural, multiplicando-o por todos os seus antecessores inteiros e maiores que zero (0). O que nos dá a seguinte fórmula: n! = n (n – 1) · (n – 2) · (n – 3) · … · 1

Então, se quero calcular o fatorial do número 5, por exemplo, basta multiplicá-lo por 4, 3, 2 e 1. Isto é: 5! = 5.4.3.2.1 = 120.

Este cálculo aparecerá em problemas de análise combinatória envolvendo os três tipos de agrupamentos que conheceremos a seguir. 

Como fazer uma análise combinatória para cada tipo de agrupamento

1. Permutação 

“Permutar” quer dizer, em termos matemáticos, trocar elementos de posição, formando, assim, uma nova ordem. E em análise combinatória, resolver um problema de permutação significa calcular quantas combinações podemos obter com todos os elementos de um conjunto. 

Porém, existem dois subtipos de permutação: a simples e a permutação com repetição. 

• Permutação simples: usa todos os elementos do conjunto, mas não admite repetição. Neste caso, fazemos o cálculo do fatorial do número natural que expressa a quantidade total de elementos do conjunto analisado. Logo, a fórmula será: Pn = n!
• Permutação com repetição: além de usar todos os elementos do conjunto, também admite repetição. Por isso, a formula contempla o número de elementos n do conjunto e as vezes que um mesmo elemento aparece no cálculo dos reagrupamentos possíveis:

 2. Arranjo: 

Neste caso, selecionamos parte dos elementos que conformam um conjunto para calcular as combinações possíveis. Isto é, aplicamos a análise combinatória para calcular a quantidade de combinações ordenadas que podemos construir com um determinado número de elementos do conjunto, que logicamente sempre deve ser menor do que a quantidade total de elementos do conjunto. 

Os arranjos também se subdividem em dois tipos, dependendo se aceitam ou não repetições. Então, temos:

• Arranjo simples: inclui todos os agrupamentos ordenados formados por um número p de elementos distintos escolhidos dentro do total de elementos do conjunto (n), ou seja, não admite repetição. Sua fórmula é:
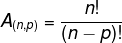
• Arranjo completo: admite repetição. Aqui, levaremos em consideração todo agrupamento de p elementos de um conjunto com n elementos diferentes, incluindo elementos repetidos, porém, considerando que a mudança de ordem determina grupos diferentes. Nestes casos, usamos a seguinte fórmula: 

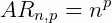
3. Combinação 

Pode parecer confuso, mas nem toda operação de análise combinatória é uma combinação, por isso, costuma-se usar o termo “reagrupamentos” mais do que “combinações”. Para esclarecer: tecnicamente, a combinação, na análise combinatória, é um tipo de agrupamento específico, no qual buscamos calcular quantos subconjuntos podemos formar a partir do total de elementos de um conjunto.  

A grande diferença entre a combinação e os outros tipos de agrupamentos é que, aqui, a ordem dos elementos não importa. Nestas situações, usamos a seguinte fórmula:

Como descobrir quantas combinações possíveis? Problemas de análise combinatória resolvidos: 

A seguir, veremos um exercício básico de contagem e um exemplo de problemas de análise combinatória resolvido para cada tipo de agrupamento. Confira e aprenda a usar as fórmulas: 

Exercício básico de contagem com diagrama de árvore 

Enunciado: Sabendo que uma moeda tem duas faces: cara (C) e coroa (K), lança-se esta moeda três vezes consecutivas e observa-se qual face ficou voltada para cima. Calcular quais e quantos são os resultados possíveis para estes lançamentos:

Resolução: Sabemos que cada etapa deste experimento tem duas possibilidades: que a moeda caia com a face da cara para cima ou que caia com a face da coroa para cima. Como a moeda foi lançada três vezes, estas possibilidades podem se repetir três vezes consecutivas, dando-nos o seguinte cálculo: 2.2.2 = 8. Ou seja, já sabemos quantos resultados possíveis temos. 

Agora, para determinar quais seriam estes resultados, uma grande ajuda é elaborar o diagrama de árvore, que também é conhecido como árvore de possibilidades. Dá uma olhada na imagem a seguir: 

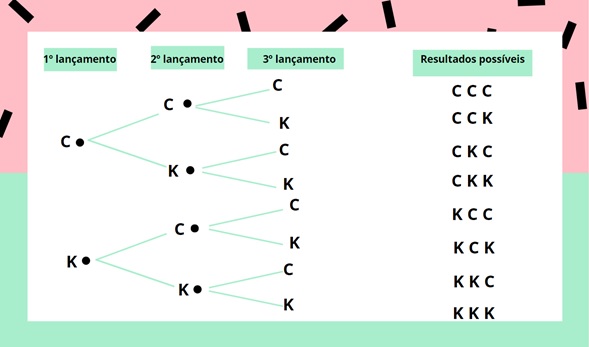
Finalmente, podemos representar o total de 8 resultados possíveis para os lançamentos em forma de conjunto da seguinte maneira: Ω = {(C, C, C); (C, C, K); (C, K, C); (C, K, K); (K, C, C); (K, C, K); (K, K, C); (K, K, K)}

Problema de Permutação com Anagramas

Enunciado: Quantos anagramas existem na palavra ROMA?

Explicação: neste caso, devemos usar todos os elementos do conjunto (que são todas as letras da palavra ROMA), e a ordem dos elementos é importante, pois, quando movemos uma letra de lugar (trocamos de posição), obtemos um novo anagrama. Logo, identificamos que se trata de uma permutação. 

Para resolver, podemos aplicar diretamente a fórmula da permutação simples para encontrar quantas possibilidades de anagrama temos na palavra ROMA ou nos basear no princípio fundamental da contagem. Entenda melhor abaixo: 

Aplicação direta da fórmula: 

Sabendo que a palavra ROMA possui quatro letras, devemos calcular o total de anagramas possíveis pela permutação de quatro elementos. Logo, a formula aplicaria ficaria assim: P4=4! = 4.3.2.1= 24 possibilidades.

Resolução detalhada pelo PFC: 

Partindo do princípio da contagem, devemos tomar quatro decisões, já que a palavra ROMA tem quatro letras, o que nos dá as seguintes possibilidades: 

• 1ª letra: Aqui temos 4 possibilidades (R, O, M, A).
• 2ª letra: Já escolhemos a primeira letra, logo, nos restam 3 possibilidades.
• 3ª letra: Como escolhemos 2 letras (uma para a primeira posição e outra para a segunda, agora temos 2 possibilidades.
• 4ª letra: Tendo escolhido as letras que ocuparão a primeira, segunda e terceira posição, só nos resta 1 possibilidade de escolha.

E novamente, caímos na fórmula: 4.3.2.1 = 24 possibilidades. 

Problema resolvido de Arranjo: Quantas combinações são possíveis com 8 números?

Enunciado: Quantos números naturais de quatro algarismos distintos podemos formar usando os algarismos 2, 3, 4, 5, 6, 7, 8 e 9?

Explicação: aqui, percebemos que a ordem dos elementos é importante, pois, quando trocamos de posição um ou mais algarismos de um número natural, obtemos outro número. Por exemplo: 2345 é diferente de 3254 e de 2453, embora todos tenham os mesmos algarismos. Logo, não se trata de uma combinação.

E como não podemos usar todos os algarismos ao mesmo tempo para formar os números, pois o enunciado nos dá a condição de usar apenas quatro, devemos usar a fórmula do Arranjo (e não da permutação). Além disso, temos um arranjo simples, pois o enunciado também nos diz que os números devem ser distintos, ou seja, que não se admite repetição.

Resolução: 

Nosso objetivo é calcular quantas combinações são possíveis com 8 números, agrupando estes números de 4 em 4. Então, aplicamos a fórmula do arranjo simples da seguinte forma: 

Conclusão: podemos formar 1.120 números naturais com os algarismos e as condições estabelecidas pelo problema. 

Problema de Combinação resolvido e explicado

Enunciado: Em uma sala de aula, temos cinco homens e sete mulheres. Quantos grupos de três homens e quatro mulheres podemos formar?

Explicação: a primeira coisa importante é perceber que, neste caso, a ordem dos elementos não é importante, pois o subconjunto formado por três ou quatro elementos do conjunto “total”, sempre serão as mesmas pessoas, independente da ordem que usemos para enumerá-las. Por exemplo: o grupo formado por Maria, Ana, Cláudia e Vitória é o mesmo que posso formar com Claudia, Ana, Vitoria e Maria. Por isso, devemos aplicar o método da combinação para resolver este problema. 

Como o enunciado nos propõe duas condições diferentes para a formação destes grupos (por um lado, que sejam de 3 homens, e por outro, que sejam de 4 mulheres), o correto é calcular separadamente as possibilidades para cada condição e, depois, multiplicar os resultados, já que cada grupo formado por homens pode se “misturar” com cada grupo de mulheres. Confira o passo a passo:

Resolução: 

1. Grupos formados por 3 homens 

Total de homens na sala (conjunto) = 5

Quantidade de homens em cada grupo (subconjunto) = 3

Aplicando a fórmula da combinação: 

 

2. Grupos formados por 4 mulheres 

Total de mulheres na sala (conjunto) = 7

Quantidade de mulheres em cada grupo (subconjunto) = 4

Aplicando novamente a fórmula de combinação: 

Desta forma, a quantidade total de grupos que podemos formar, seguindo as condições estabelecidas, é de:

C5,3 · C7,4 = 10 · 35 = 350 possibilidades

Para mais explicações e problemas de análise combinatória resolvidos:

Para se aprofundar nos tipos de agrupamentos da análise combinatória e ver o passo a passo para resolver problemas comuns em provas e concursos, não deixe de conferir estes vídeos: 

1. Introdução à Análise Combinatória e Probabilidade – De Descomplica

 

2. Permutação, Arranjo e Combinação: como saber quando usar cada um? – De Matemática Genial  

3. Arranjos Simples e com Repetição – De Prof. Estrada

4. Permutação Simples e com Repetição – De Brasil Escola

 

5. Maratona de Exercícios para aprender Análise Combinatória – De DicasMat Sandro Curió

Precisa de ajuda para fazer análise combinatória?

Como falamos lá na introdução, a análise combinatória é aplicada em vários processos e estudos dentro da própria Matemática e também de outras áreas, como saúde, ciência, estatística, economia, etc. Nestes casos, geralmente, se analisam populações ou amostras muito maiores e condições mais específicas do que aquelas que vimos nos problemas anteriores. 

Obviamente, isto significa ter que desenvolver cálculos e análises de dados muito mais complexos, que requerem habilidades e conhecimentos específicos, além de uma manipulação de ferramentas e programas informáticos que facilitam estes cálculos e a organização e a interpretação dos resultados obtidos a partir deles. 

Se esse é o seu caso e você precisa de ajuda para resolver problemas mais complexos de análise combinatória, a melhor opção é solicitar a ajuda de um profissional. Lembre-se que, na Workana, oferecemos um Diretório de freelancers diversificado, onde você encontra profissionais independentes especializados em matemáticas e análise combinatória, estatísticas e muitas outras áreas de Finanças e Administração.   

Mas, se você ainda não sabe exatamente quais habilidades são necessárias para o ótimo desenvolvimento da sua ideia ou do seu empreendimento, basta publicar um projeto grátis para começar a receber propostas dos nossos profissionais. Converse com eles/elas, explique a sua demanda, negocie o orçamento e dê o próximo passo! 

—

Estes artigos também podem ser úteis:

• Repensando TI: porque precisamos continuar falando sobre tecnologia da informação nos próximos anos
• Descobrir oportunidades ocultas: Capital Humano com Freelancers para fortalecer suas equipes
• Prepare-se para o fim do ano com o impulso de uma equipe de suporte distribuído
• Empreendedor: já sabe tudo que um assistente virtual pode fazer pelo seu negócio?
• Quais são os processos de recrutamento mais eficazes para atrair talentos de TI?
• Tudo que você precisa saber se sua primeira experiência com um freelancer não foi como você esperava